Was ist der "ungünstigste Punkt" – und wo liegt er überhaupt?

Da widersprechen sich die Experten

Bei einer Grundwasserabsenkung geht man nach Herth/Arndts¹ so vor: Nach der Festlegung der Vorwerte, wie der Art des Grundwasserleiters, dem k-Wert, der Absenktiefe, der Eintauchtiefe der Brunnen und eventueller Zuschläge zum Wasserandrang, wird der Wasserandrang zum Absenktrichter berechnet. Danach wird das Fassungsvermögen des Einzelbrunnens bestimmt und daraus ergibt sich durch Division die Anzahl der benötigten Brunnen.

"Die Brunnen sind um die Baugrube zu verteilen. […] Bei optimaler Brunnenverteilung ist die Ergiebigkeit der einzelnen Brunnen, absolut homogener Untergrund vorausgesetzt, theoretisch gleich groß. Dieser Zustand ist in der Praxis nicht vorhanden. […] Es wird jetzt mit der Mehrbrunnenformel die Wassermenge […] für die ungünstigsten Punkte in der Baugrube (Hrvbg. von mir) mit den gleichen Ausgangswerten mit Ausnahme von A_RE neu ermittelt. Jetzt wird überprüft, ob die vorgesehene Anlage die neue Wassermenge einschließlich der Zuschläge fassen kann. Danach können mit der allgemeinen Brunnenformel [...] weitere Punkte des Absenktrichters berechnet werden.“²

Wo die ungünstigen Punkte zu suchen sind, darüber sind sich die Autoren uneins, denn wir finden in der Literatur dazu (wenigstens) zwei Ansichten, die sich widersprechen:

• „Der Mittelpunkt der Baugrube ist der ungünstigste Punkt der Absenkung.“³
• „Kontrolle des Wasserstandes an der ungünstigsten Stelle. Diese soll in Baugrubenmitte liegen.“⁴
• „Nachweis der Grundwasserabsenkung in der Baugrubenmitte..“⁵
• „Es genügt … im allgemeinen, die nachstehend folgende Rechnung für den ungünstigsten Punkt, der normalerweise an einer äußeren Ecke der Baugrube liegt, durchzuführen.“⁶

Wo also liegt der ungünstigste Punkt? Immer in der Mitte der Baugrube oder normalerweise am Rand und was heißt dann „normalerweise“? Und: Meinen die Autoren auch das Gleiche, wenn sie den gleichen Begriff verwenden?

"Ungünstig" kann ein Punkt im Absenkgebiet nämlich in zweifacher Hinsicht sein:

• Ein Punkt ist ungünstig, wenn in ihm die Absenkung bei gegebener Fördermenge Q minimal ist.
• Ein Punkt ist ungünstig, wenn die zu fördernde Wassermenge Q, die notwendig ist, um das Absenkziel in diesem Punkt zu erreichen, maximal wird.

 

Wo wird der Wasserandrang maximal?

Für den Wasserandrang zu einem Punkt im Feld einer Mehrbrunnenanlage gilt bei freier Oberfläche bekanntlich: $$Q=\frac{\pi \cdot k\cdot ({{H}^{2}}-{{h}^{2}})}{ln\left( \frac{R}{r} \right)} = \frac{\pi \cdot k\cdot ({{H}^{2}}-{{h}^{2}})}{ln(R)-ln({{A}_{\operatorname{Re}}})}$$ wobei sich A_RE aus den Logarithmen der Entfernungen zu den Brunnen berechnet. Daraus folgt aber sofort: Je größer A_RE ist, desto kleiner der Nenner des Bruchs und desto größer wird Q.

Der für den Wasserandrang ungünstigste Punkt ist der Punkt mit dem maximalen lokalen Ersatzradius.

Eine mit GwR erstellte Grafik bestätigt diese Überlegung: Der Graph der Funktion A_RE → Q(A_RE) ist für A_RE < R monoton steigend (offenbar ist A_RE = R eine Polstelle).

 

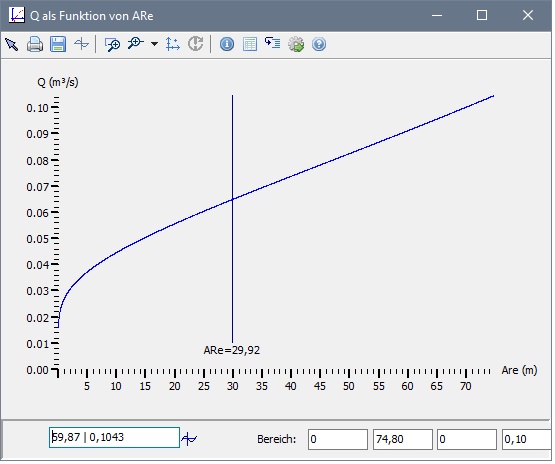
Wo wird die Absenkung minimal?

Betrachten wir nun die erzielte Absenkung; eine Bemessungswassermenge Q sei festgelegt, wo ist dann die erzielte Absenkung minimal? Für die Spiegelfläche gilt bei freier Oberfläche

$${{y}^{2}}={{H}^{2}}-\frac{Q}{\pi \cdot k}\left[ \ln \,R-\frac{1}{n}\cdot \ln \left( {{x}_{1}}\cdot {{x}_{2}}\cdot ...\cdot {{x}_{n}} \right) \right]$$

Der Wasserstand an einer beliebigen Stelle einer Mehrbrunnenanlage hängt bis auf konstante Terme vom Produkt der Entfernungen von der Stelle zu den Brunnen ab.

Die in einem Punkt P im Absenkgebiet (mit dem lokalen Ersatzradius A_ARE) erzielte Absenkung ist dann

$$s(P)=H-\sqrt{\ {{H}^{2}}-\frac{Q}{\pi \cdot k}\cdot \frac{ln({{R}_{Bem}})}{ln\left( {{A}_{RE}} \right)}}$$

Daraus folgt aber sofort: Je größer A_RE ist, desto größer ist der Wert der Wurzel und desto kleiner wird s.

Der für die erzielte Absenkung ungünstigste Punkt ist der Punkt mit dem maximalen lokalen Ersatzradius.

Die oben unterschiedenen ungünstigen Punkte fallen also zusammen.

 

Und wo liegt er nun?

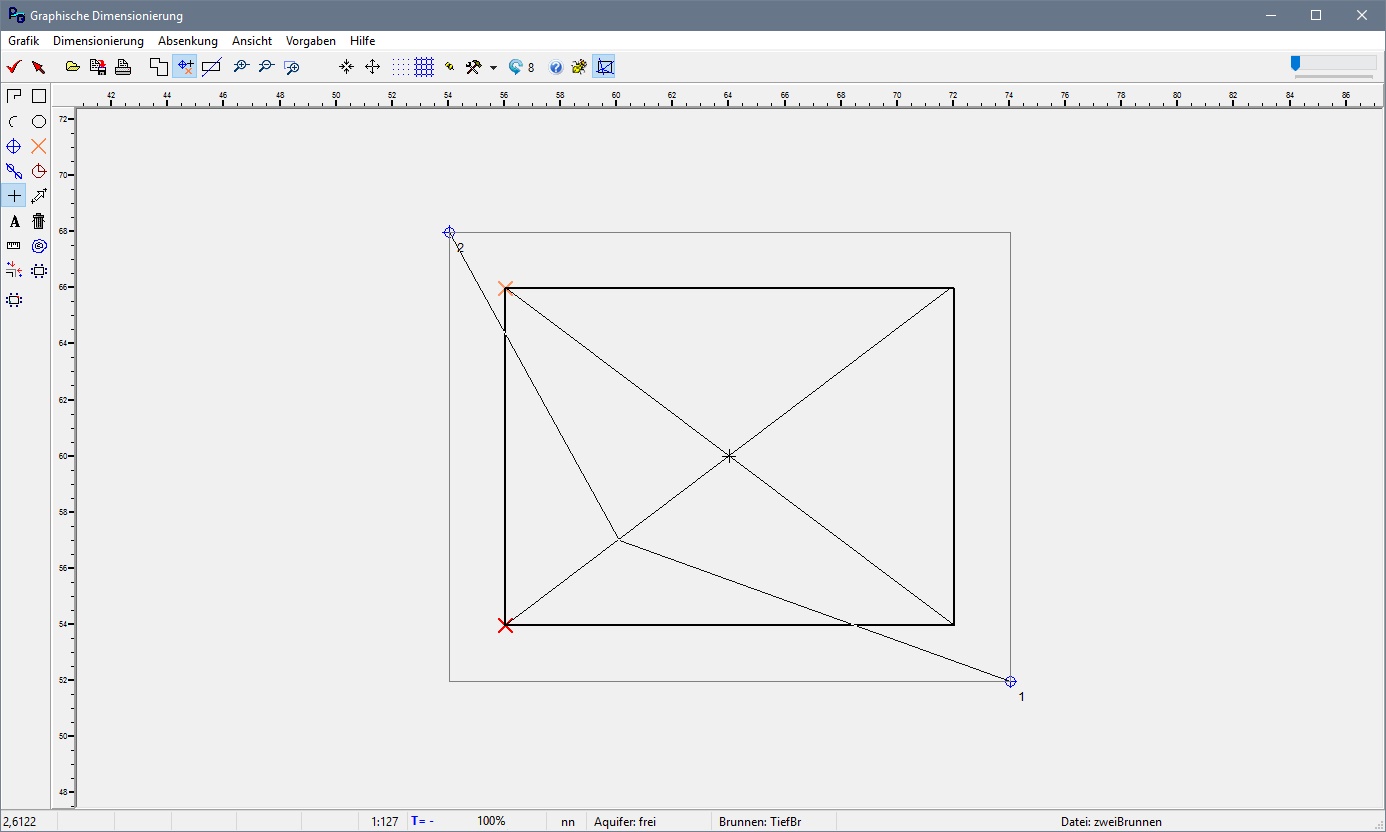
Wir betrachten eine Baugrube mit zwei gegenüber liegenden Brunnnen und einen Punkt, der von der Baugrubenmitte aus auf einer Diagonalen zur unteren linken Ecke wandert. In der Baugrubenmitte sind die Entfernungen x₁, x₂ zu den beiden Brunnen minimal. Je weiter man auf der Diagonalen nach unten links (oder rechts oben) wandert, desto größer werden x₁ und x₂ und damit ln(x₁·x₂) und deswegen liegt der ungünstigste Punkt hier nicht in der Baugrubenmitte (dort liegt der günstigste Punkt), sondern im unteren linken Eck der Baugrube..

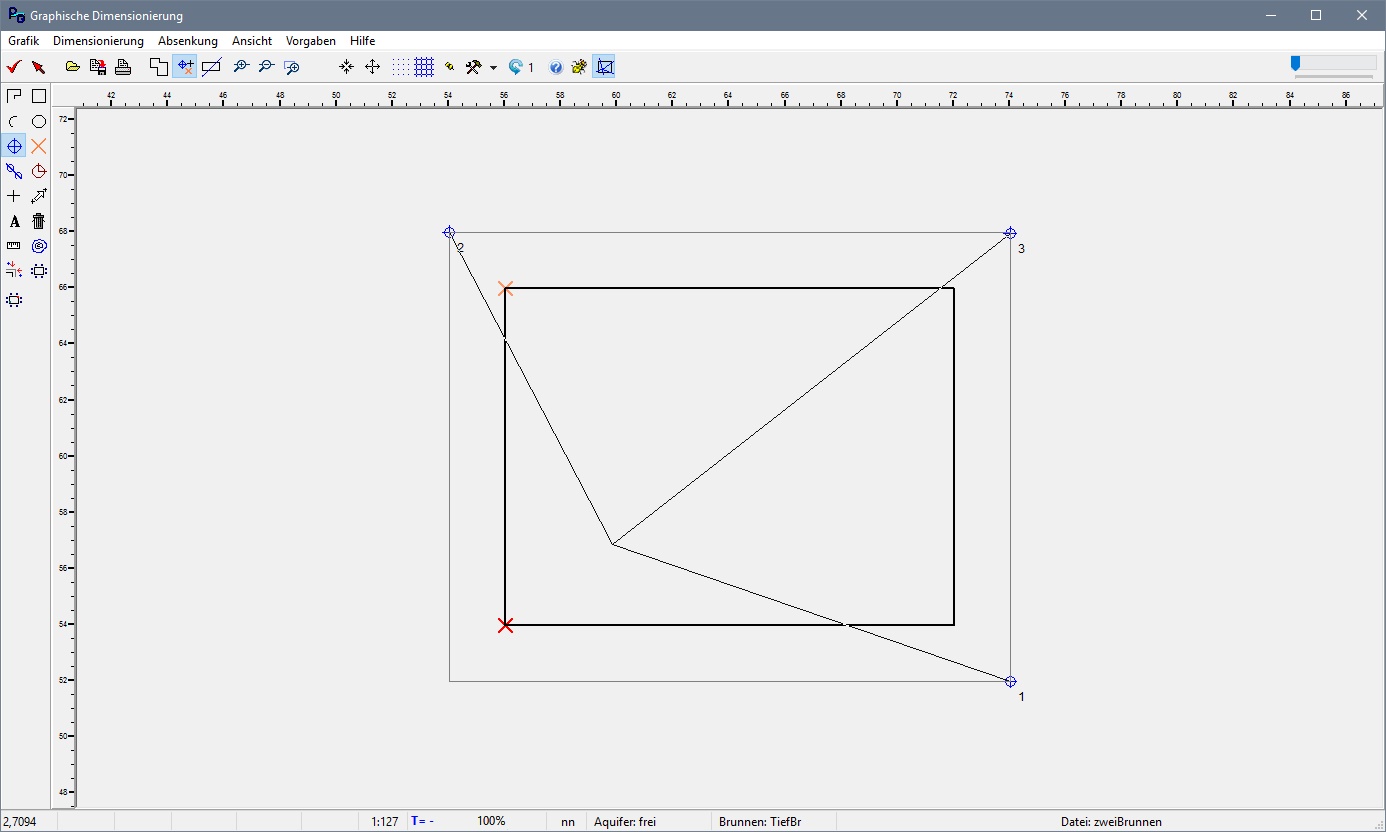
Fügen wir einen dritten Brunnen hinzu, so wird es noch deutlicher: die Strecken x₁, ... , x₃ sind in der linken unteren Ecke maximal lang, dort ist der ungünstigste Punkt und dort findet ihn ProAqua.

Ein Fazit

Die Behauptung, dass der ungünstigste Punkt in der Baugruppenmitte zu suchen sei, ist nicht haltbar, dort ist der günstigste Punkt. Der ungünstigste Punkt liegt auf der Baugrubenperipherie, häufig auf einer Ecke der Baugrube.

 

---