Info
Tipp: Mit der rechten Maustaste über einer Formel öffnen Sie ein Kontextmenü.
Formelsammlung Grundwasserabsenkung nach Herth/Arndts
» Formelsammlung als PDF-Datei herunterladen.
Version 1.8.6a (16.08.22), © Dr. Georg Schöffel, 2011-22.
ProAqua und GwR beruhen auf den Berechnungsmethoden,
die in dem Standardwerk von Herth/Arndts dargestellt sind. Hier werden
die wichtigsten Formeln zusammengestellt, die in ProAqua benutzt werden. Die in Klammern angegebene Zahl ist die Formelnummer,
danach folgt die Seitenzahl. Hinweise auf Fehler oder Ergänzungsvorschläge

Haftungsausschluss: Es wird keinerlei Garantie für die Richtigkeit der Formeln übernommen, nicht einmal dafür, dass sie fehlerfrei aus der Literatur übertragen oder umgeformt wurden. » Bekannte Fehler
- Bezeichnungen
- Reichweitenformeln
- Ersatzradius einer Baugrube
- Wasserandrang (Tiefbrunnen)
- Absenkung in der Entfernung x (Tiefbrunnen)
- Vorlaufzeit
- Tiefbrunnen
- Vakuumtiefbrunnen
- Dimensionierung einer Absenkung mit Tiefbrunnen
- Wasserandrang (Sickerschlitze)
- Absenkung in der Entfernung x (Sickerschlitze)
- Wasserandrang zu einer Baugrube nach Davidenkoff
- Berechnung des k-Wertes
1 Bezeichnungen
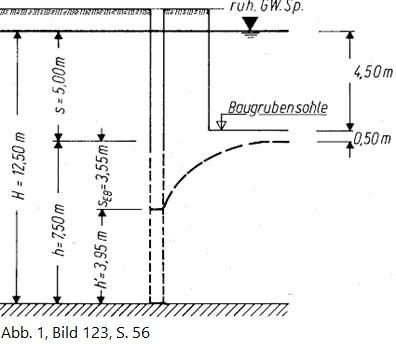
H = s + h
H = s + sEB + h'
0,1 ≤ pfrei ≤ 0,3 Mittelwert: 0,2
0,0001 ≤ pgesp ≤ 0,005 Mittelwert: 0,00255
2 Reichweitenformeln
$$R = {3000 \cdot s \cdot \sqrt{k}}$$
Bei Sickerschlitzen wird R mit dem Faktor 1500 bis 2000 (vgl. Herth/Arndts, S. 139) berechnet.
$$ R = {575 \cdot s \cdot \sqrt{k \cdot H}}$$
$$R = {575 \cdot s \cdot \sqrt{k \cdot m}}$$
$$R_W = {\sqrt{R^2 + A^2_{RE}}}$$
$$ R = {1,5 \cdot \sqrt{ {k \cdot H \cdot t} \over p}}$$
Nach einem Vorschlag von Weyrauch werden für t und p Standardwerte wie folgt gesetzt: t = 30 Tage = 2.592.000 s, p = 0,2. Dadurch vereinfacht sich die Formel zu: $$R = {5400 \cdot \sqrt{k \cdot H}}$$ Wird die Reichweite als Minimalreichweite berechnet, so treten die Anomalien der Funktion s → Q(s) nicht auf (vgl. Weyrauch/Schöffel).
Berechnet man die Vorlaufzeit mit der Minimalreichweite, so erhält man die gewählte Zeit t.
$$R = {1,5 \cdot \sqrt{ {k \cdot m \cdot t} \over p}}$$
Nach einem Vorschlag von Weyrauch werden für t und p Standardwerte wie folgt gesetzt: t = 1,5 Tage = 129.600 s, p = 0,0009. Dadurch vereinfacht sich die Formel zu: $$R = {18000 \cdot \sqrt{k \cdot m}}$$ Wird die Reichweite als Minimalreichweite berechnet, so treten die Anomalien der Funktion s → Q(s) nicht auf (vgl. Weyrauch/Schöffel).
Berechnet man die Vorlaufzeit mit der Minimalreichweite, so erhält man die gewählte Zeit t.
freie Oberfläche: $$R_t = {c_r \cdot \sqrt{ {k \cdot H \cdot t} \over p}}$$ gespannte Oberfläche: $$R_t = {c_r \cdot \sqrt{ {k \cdot m \cdot t} \over p}}$$
cR ergibt sich aus der tolerierten Restabsenkung sR am Trichterrand und wird wie folgt berechnet.
freie Oberfläche:
$$ R_t = 2 \cdot \sqrt{ {{ k \cdot H \cdot t} \over p } \cdot ln \left( {Q \over Q_R} \right) } = 2 \cdot \sqrt{ {{ k \cdot H \cdot t} \over p } \cdot ln \left( {100 \over p_{Rest}} \right) } $$
gespannte Oberfläche :
$$ R_t = 2 \cdot \sqrt{ {{ k \cdot m \cdot t} \over p } \cdot ln \left( {Q \over Q_R} \right) } = 2 \cdot \sqrt{ {{ k \cdot m \cdot t} \over p } \cdot ln \left( {100 \over p_{Rest}} \right) } $$
mit: \(Q_R = { P_{Rest} \over 100} \cdot Q \)
3 Ersatzradius einer Baugrube
dBrGr = Abstand der Brunnen vom Grubenrand
$$A_{RE} = \sqrt{A_{Absenk} \over \pi}$$
Ist a die längere Seite der umschlossenen Fläche, so wird abhängig vom Seitenverhältnis \(m = \frac{a}{b}\) aus einem Diagramm der Wert η abgelesen. Damit gilt für ARE:
$${{A}_{RE}}=\eta \cdot b$$
Nach anderen Quellen gilt für η näherungsweise (1 ≤ m ≤ 7) : $$\eta = 0,2\cdot \frac{a}{b}+0,37$$ Also: $${{A}_{RE}} = 0,2\cdot{a}+0,37\cdot{b}$$
Wird der Ersatzradius als Radius eines Kreises bestimmt, so ist eine Baugrube langgestreckt, wenn m > 3 ist (m ist im vorigen
Abschnitt definiert). Wird die η-Methode benutzt, dann ist eine Baugrube langgestreckt, wenn m > 7. Für eine langgestreckte
Baugrube gilt:
$$A_{RE} = {1 \over 3} \cdot \left( L_{Gr}+2d_{BrGr}\right)$$
$$A_{RE}(P) = e^{{1 \over n} \sum \limits_{i=1}^n {ln x_i}}$$
P ein Punkt im Absenkgebiet
n Brunnenzahl
xi Abstand des Punktes P vom i-ten Brunnen
4 Wasserandrang (Tiefbrunnen)
4.1 Freie Oberfläche
$$Q = {{\pi \cdot k \cdot \left( H^2 - h^2 \right) } \over {ln \left({R \over r}\right)} } $$
Es ist: r = ARE. Da h = H - s, gilt: H2 - h2 = 2Hs-s2
- Q wächst linear mit H.
- Q hat genau eine Polstelle mit VZW: \( {ln \left( 3000 \cdot s \cdot \sqrt k \over A_{RE} \right) = 0 } \Longleftrightarrow s = {A_{RE} \over 3000 \cdot \sqrt k} \). Für noch kleinere Werte von s (letzte Formel) wird Q negativ.
Wenn \(0 < ln\left(R \over A_{RE} \right) < 1, \) dann setzte
$$Q = \pi \cdot k \cdot \left(H^2 - h^2 \right) \cdot \left( 2{ A_{RE} \over R }+ 0,25\right)$$
- Nach Weyrauch wird also in der Formel für Q \( 1 \over { ln\left(R \over A_{RE} \right) } \) durch \(2 \cdot { A_{RE} \over R }+ 0,25 \) ersetzt.
- Es gilt: \( ln\left(R \over A_{RE} \right) < 1 \Longleftrightarrow R < e \cdot A_{RE} \approx 2,7 \cdot A_{RE} \). Merke: "Kleine Reichweite bei großer Baugrube".
- Mit der Weyrauch-Näherung geht Q(s) für s→0 nicht gegen 0, wie es sein müsste, sondern gegen \( {\pi \cdot A_{RE} \cdot H \cdot \sqrt k} \over 750\). Nur bei Verwendung der Minimalreichweite (vgl. Weyrauch/Schöffel) wird dieser Fehler vermieden.
- Genau genommen ist dies die Herth/Arndts - Interpretation eines Vorschlags von Weyrauch, der auf etwas anderes zielte. Genaueres dazu im Aufsatz Weyrauch/Schöffel oder unter Weyrauch-Näherung.
4.2 Gespannte Oberfläche
$$Q = {{2 \cdot \pi \cdot k \cdot m \cdot s } \over {ln \left({R \over r}\right)} }$$
- Genau wie Qfrei(s) hat die Funktion eine Polstelle bei: \( s = {A_{RE} \over 3000 \cdot \sqrt k} \). Für noch kleinere Werte von s wird Q negativ.
- Strebt die Dicke m' der undurchlässigen Deckschicht gegen 0, so konvergiert Qgesp nicht gegen Qfrei, wie es eigentlich sein müsste, sondern gegen \( {2 \cdot \pi \cdot k \cdot T \cdot s } \over { ln \left({R \over r}\right) }\) > Qfrei = \( {2 \cdot \pi \cdot k \cdot T \cdot s - \pi \cdot k \cdot s^2 } \over { ln \left({R \over r}\right) }\).
Wenn \(0 < ln\left(R \over A_{RE} \right) < 1, \) dann setzte $$Q = 2 \cdot \pi \cdot k \cdot m \cdot s \cdot \left( 2 \cdot { A_{RE} \over R }+ 0,25\right)$$
4.3 Übergang gespannte und freie Oberfläche
- Man spricht vom "Übergang zwischen gespannter und freier Oberfläche", wenn die Absenktiefe den durchlässigen Horizont erfasst.
- \(Q={{Q}_{frei}}-\frac{\pi \cdot k\cdot {{\left( H-m \right)}^{2}}}{ln\left( \frac{R}{r} \right)} = {{Q}_{frei}}-\frac{\pi \cdot k\cdot m_{u}^{2}}{ln\left( \frac{R}{r} \right)}\).
- Bei gleichen Parametern gilt: Qfrei > Qgesp > QÜbergang .
4.4 Halbgespannte Oberfläche
$$ \begin{align} Q &=2 \cdot \pi \cdot k\cdot s \cdot \frac{{{A}_{RE}}}{\lambda }\cdot \frac{{{K}_{1}}\left( \frac{{{A}_{RE}}}{\lambda } \right)}{{{K}_{0}}\left( \frac{{{A}_{RE}}}{\lambda } \right)} \\ \lambda &= \sqrt{\ \frac{k}{k'}\cdot m\cdot m'} \end{align} $$
m' und k' gehören zur oberen, weniger durchlässigen Schicht.
4.5 Zuschlag zum Wasserandrang wegen eines nahen Gewässers
$${{Q}^{+}}=\frac{\pi \cdot k\cdot ({{H}^{2}}-{{h}^{2}})}{ln\left( \frac{c\cdot {{e}_{Gew}}}{{{A}_{RE}}} \right)}$$
Lokale Baugrube neben dem Gewässer: c = 2,
Langestreckte Baugrube parallel dazu: c = 1
- Statt R wird die gewichtete Entfernung deff = c·eGew zum Gewässer eingesetzt.
- Bedingungen (sonst wird (Z < 0):
- 0 ≤ ARE < R; 0 ≤ ARE < c·eGew
- 0 ≤ c·eGew < R
- Der Zuschlag wird genau dann 0, wenn deff = R.
- \({{Q}^{+}}={{Q}_{frei}}\cdot \frac{ln\left( \frac{R}{{{A}_{RE}}} \right)}{ln\left( \frac{c\cdot {{e}_{Gew}}}{{{A}_{RE}}} \right)}\) Zuschlag in % = \(\left( \frac{ln\left( \frac{R}{{{A}_{RE}}} \right)}{ln\left( \frac{c\cdot {{e}_{Gew}}}{{{A}_{RE}}} \right)}-1 \right)\cdot 100\).
5 Absenkung in der Entfernung x (Tiefbrunnen)
Hinweis: x wird auf die Baugrubenmitte bezogen.$$s(x)=H-\sqrt{\ \frac{Q}{\pi \cdot k}\cdot ln\left( \frac{x}{{{A}_{RE}}} \right)+{{(H-s)}^{2}}}$$
$$s(x)=H-\frac{Q}{2\pi \cdot k\cdot m}\cdot ln\left( \frac{x}{{{A}_{RE}}} \right)$$
$$ \begin{align} a &=\frac{({{m}^{2}}-{{h}^{2}})\cdot ln(R)+2\cdot m\cdot (H-m)\cdot ln({{A}_{RE}})}{2\cdot m\cdot (H-m)+{{m}^{2}}-{{h}^{2}}} \\ \\ s(x)&= \cases{ s(x)_{frei} & x < a\cr s(x)_{gespannt} & x ≥ a } \end{align} $$
$$s(x)=\frac{Q}{2\cdot \pi \cdot k\cdot m}\cdot \frac{\lambda }{{{A}_{RE}}}\cdot \frac{{{K}_{0}}\left( \frac{x}{\lambda } \right)}{{{K}_{1}}\left( \frac{{{A}_{RE}}}{\lambda } \right)}$$
6 Vorlaufzeit
Die Vorlaufzeit ist die Zeit, die bis zum Erreichen des Absenkziels vergeht. Das Absenkziel ist erreicht, wenn in der Entfernung ARE von der Baugrubenmitte aus die Sollabsenkung s erreicht ist.
Die Gleichung der zeitlichen Absenkung lautet: $$ \begin{align} s(x,t)&=S+\beta \cdot ln(t)-\alpha \cdot ln(x) \\ S&=\beta \cdot ln\left( \frac{2,25\cdot k\cdot m}{p} \right) \\ \alpha &=2 \cdot \beta \\ \beta &=\frac{Q}{4\cdot \pi \cdot k\cdot m} \end{align} $$
Auflösung nach t ergibt: t = eA mit: \(A=\frac{{{s}}}{\beta }\ +\ ln\ \left( \frac{A_{\operatorname{Re}}^{2}\cdot p}{2,25\cdot k\cdot m} \right)\)
Bei freiem Spiegel wird \(s = s_u = {{H^2-h^2} \over {2 \cdot H}} \) gesetzt; su wird reduzierte Absenkung genannt. Auflösung nach t ergibt: t = eA mit: \(A=\frac{{{s}_{u}}}{\beta }\ +\ ln\ \left( \frac{A_{\operatorname{Re}}^{2}\cdot p}{2,25\cdot k\cdot H} \right)\)
Vgl. Beispiel 10, S. 293ff.
7 Tiefbrunnen
7.1 Fassungsvermögen, Filterstrecke, sEB
h' = h-sEB
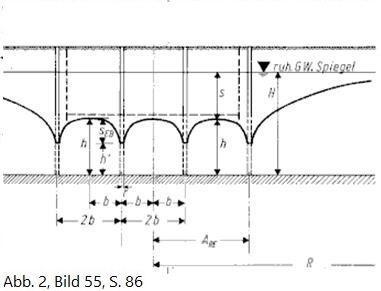
b = halber mittlerer Brunnenabstand einer Mehrbrunnenanlage
r = wirksamer Brunnenradius
Setzt man \(q=\frac{Q}{n}\)und Q (ohne Zuschläge) entsprechend ein, so erhält man: \({{s}_{EB}}=\ \,\frac{1,5\cdot s}{n}\cdot \frac{ln\left( \frac{b}{r} \right)}{ln\left( \frac{R}{{{A}_{RE}}} \right)}\).
sEB ist also unabhängig von m (bei Sichardt-Reichweite).
7.2 Maximale Absenkung und Kapazität des Einzelbrunnens
Bei Verwendung der Minimalreichweite oder einer konstanten Reichweite kann die Gleichung algebraisch gelöst werden. Sonst ist eine nummerische Lösung möglich. Mit smax kann dann die Kapazität berechnet werden.
7.3 Unvollkommene Brunnen
Mit \(a = T - H \) gilt: $$ {Q}_{unvk}(H,T)=\left\{ \begin{align} & 1,1\cdot Q_{vollk}(H,H)\quad 0 < a\le H \\ & 1,2\cdot Q_{vollk}(H,H)\quad H < a < 2\cdot H \\ & 1,3\cdot Q_{vollk}(H,H)\quad a \ge 2 \cdot H \\ \end{align} \right. $$
8 Vakuumtiefbrunnen
qV = Ergiebigkeit des Vakuumbrunnens
q = Ergiebigkeit ohne Vakuum
\(\vartheta \) = empirischer Faktor (= 15)
\(U=\frac{{{d}_{60}}}{{{d}_{10}}}\)
pV = Unterdruck im Brunnen
Der wirksame Brunnenradius ist ungefähr die Entfernung von der Brunnenmitte, in der "der wirksame Unterdruck noch etwa 50 cm Wassersäule" beträgt (S. 76).
r·pmax = x1· p1 = xn· pn
Für den wirksamen Radius eines Vakuumtiefbrunnes gilt also:
$${{r}_{wirk}}=\frac{{{r}_{Br}}\cdot {{p}_{eff}}}{{{p}_{\max }}}=\frac{{{r}_{Br}}\cdot {{p}_{eff}}}{0,049}$$
\({{k}_{Luft}}=\frac{70}{3}\cdot k\)
9 Dimensionierung einer Absenkung mit Tiefbrunnen
- Qmax berechnen, n schätzen ⇒ h'vdh
- Sichardt-Formel für das Fassungsvermögen ⇒ h'erf
- Reserveh = h vdh - h erf bzw.
Reserveq = q vdh - q erfsub>
10 Wasserandrang (Sickerschlitze)
10.1 Vollkommene Schlitze (Dupuit, Thiem)
Die Formeln berechnen den einseitigen Zufluss zu einem Meter Schlitz. Bei zweiseitigem Zufluss wird die Wassermenge verdoppelt. R wird mit dem Faktor 1500 bis 2000 (vgl. Herth/Arndts, S.139) berechnet.
10.2 Unvollkommene Schlitze
Für einen Einzelschlitz mit einseitigem Zufluss gilt:
$${{t}_{d}}={{t}_{0}}\cdot \left( \frac{1,48}{R} \cdot (T-{{t}_{0}})+1 \right)$$Bei parallelen Schlitzen mit beidseitigem Zufluss gilt:
$${{t}_{d}}={{t}_{0}}\cdot \left( \frac{{{C}_{1}}\cdot {{C}_{2}}}{R}\cdot(T-{{t}_{0}})+1 \right)$$Die Formel berechnet den einseitigen Zufluss zu einem Meter Schlitz. Bei zweiseitigem Zufluss wird die Wassermenge verdoppelt und td auf andere Art berechnet.
C1, C2 sind aus Diagrammen (Abb. 91, 92, S. 144) zu entnehmen.
$$q=\frac{k\cdot m\cdot (T-{{t}_{e}})}{R+ℓ}$$
Beidseitiger Zufluss:
$$q=\frac{2\cdot k\cdot m\cdot (T-{{t}_{e}})}{R+\lambda \cdot m}$$
(165) S. 144; λ ist einem Diagramm (Abb. 95, S. 146) zu entnehmen.
(164) S. 143
11 Absenkung in der Entfernung x (Sickerschlitze)
Hinweis: x wird auf die Baugrubenmitte bezogen.s(x) ist linear in x: \(s(x)=\left( -\frac{q}{k\cdot m} \right)\cdot x+\frac{R \cdot q}{k \cdot m}\).
$$ \begin{align} a &=\frac{R\cdot \left( {{m}^{2}}-{{h}^{2}} \right)}{2\cdot m\cdot (H-m)+{{m}^{2}}-{{h}^{2}}} \\ \\ s(x)&= \cases{ s(x)_{frei} & x < a\cr s(x)_{gespannt} & x ≥ a } \end{align} $$
\(s(x)=\frac{\left( T-{{t}_{e}} \right)\cdot (R-x)}{R+\lambda \cdot m}\) s(x) ist linear in x: \(s(x)=\left( \frac{{{t}_{e}}-T}{R+\lambda \cdot m} \right)\cdot x-\frac{\left( {{t}_{e}}-T \right)\cdot R}{R+\lambda \cdot m}\).
12 Wasserandrang zu einer Baugrube nach Davidenkoff
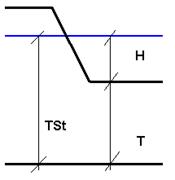
$$Q=k \cdot {{H}^{2}} \cdot \left[ \left( 1+\frac{t}{H} \right)\cdot m+\frac{{{L}_{1}}}{R}\cdot \left( 1+\frac{t}{H}\cdot n \right) \right]$$ $$t = min ( H, T )$$
- Die Bedeutung der Größen T und H weicht von der üblichen Bedeutung bei Tiefbrunnen ab. \(t = \cases{ H & T ≥ H \cr T & T < H \cr }\)
- m und n sind einem Diagramm (Abb. 99, S. 147) zu entnehmen.
- R. Rieß, Grundwasserströmung – Grundwasserhaltung. Grundbautaschenbuch, 5(1996) Bd. 2, S. 365–499, Berlin: Ernst & Sohn, S. 386.
13 Berechnung des k-Wertes
c ist einem Diagramm (Abb. 63, S. 93) in Abhängigkeit vom Ungleichförmigkeitsfaktor U zu entnehmen. \(U = \frac{{{d}_{60}}}{{{d}_{10}}}\)
Fehler in früheren Versionen
- In den Versionen v1.0 - v1.8 (05.09.19) hieß es im Kommentar zum Wasserandrang bei freier Oberfläche (4.1): "Q wächst linear mit H und k." Das ist offenbar falsch.
- In den Versionen v1.0 - v1.8.1 (18.10.19) war die Formel für die Absenkung in der Entfernung x für die halbgespannte Oberfläche falsch.
- In den Versionen v1.7 - v1.8.6 (02.10.21) war der Faktor in der vereinfachten Formel für die gespannte Minimalreichweite mit 1800 angegeben; richtig ist aber 18000. Vielen Dank an einen aufmerksamen Benutzer. Der Fehler wurde in der Version 1.8.6a (16.08.22) korrigiert.