Die Weyrauch-Näherung
» Diesen Beitrag als PDF-Datei herunterladen.
Was ist die Weyrauch-Näherung?
In Herth/Arndts wird die Weyrauch-Näherung als eine Lösung des Anomalien-Problems angeboten. Bei bestimmten Bedingungen kann es vorkommen, dass "die Zuströmung Q mit kleiner werdenden Absenkungen größer wird. ... Weyrauch schlägt in einer nicht veröffentlichten Arbeit vor, in derartigen Fällen für den Wert $$\frac{1}{2,3\left( \lg \ R-\lg \ {{A}_{RE}} \right)}=2\cdot \frac{{{A}_{RE}}}{R}+0,25$$ zu setzen, der empirisch gefunden worden ist" (S. 90). Der Vorschlag lautet, Q als eine abschnittsweise definierte Funktion festzulegen:
$$Q=\left \{ \begin{aligned} & \frac{\pi \cdot k \cdot \left( {{H}^{2}}-{{h}^{2} } \right)}{ln \left( \frac{R}{{{A}_{RE}}} \right)} &ln \left( \frac{R}{{{A}_{RE}}} \right) \ge 1 \\ & \pi \cdot k \cdot \left( {{H}^{2}}-{{h}^{2}} \right) \cdot \left( 2\cdot \frac{{{A}_{RE}}}{R}+0,25 \right) &ln \left( \frac{R}{{{A}_{RE}}} \right) < 1 \\ \end{aligned} \right.$$Nun meint "empirisch gefunden" nach üblichem Sprachgebrauch: es wurden Messungen durchgeführt und daraus ging die Formel hervor. Im Falle der Weyrauch-Formel entspricht dies aber nicht den Tatsachen1, denn der Funktionsterm ergibt sich als eine innerhalb gewisser Grenzen hinreichend genaue lineare Näherung der logarithmischen Kurve \(x\to \frac{1}{ln\left( \frac{1}{x} \right)} = - \frac{1}{ln(x)}\), die in der Dupuit-Thiemschen Formel mit \(x=\frac{{{A}_{RE}}}{R}\) auftritt.
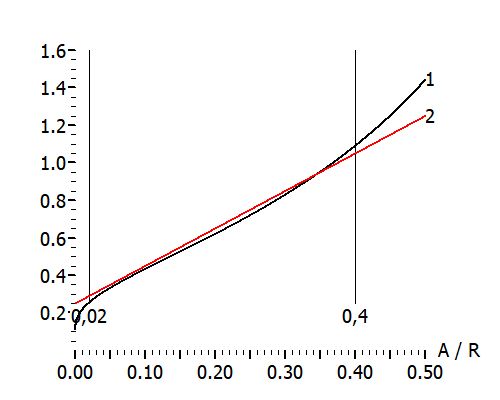
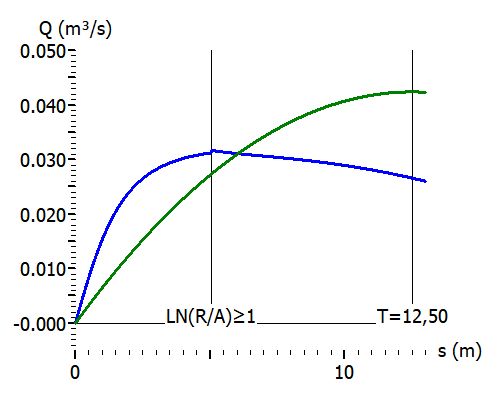
Die Abbildung zeigt den Graphen der logarithmischen Kurve (1) und den der linearen Funktion, die durch y = 2 ⋅ x + 0,25 (2) gegeben ist.
Für 0,02 < x < 0,4 approximiert die lineare Funktion die logarithmische mit einer Genauigkeit, die innerhalb der Grenzen der sonstigen Parameter liegt. Welche Grenzen erhält man damit für \( ln \left( \frac{R}{{{A}_{RE}}} \right) \)? $$\begin{align} & \quad \quad 0,02\text{ }<\text{ }\frac{{{A}_{RE}}}{R}\text{ }<\text{ }0,4 \quad \quad \quad |\hat{\ }(-1) \\ & \Leftrightarrow \frac{1}{0,02}\ \,>\ \ \frac{R}{{{A}_{RE}}}\ \ \,>\frac{1}{0,4} \quad \quad | \; ln \\ & \Leftrightarrow ln\left( \frac{1}{0,02} \right) \,>\ \ ln\left( \frac{R}{{{A}_{RE}}} \right) \,>ln\left( \frac{1}{0,4} \right) \\ & \Leftrightarrow 3,91\ >\quad ln\left( \frac{R}{{{A}_{RE}}} \right)\ >\quad 0,91\approx 1 \\ \end{align}$$
Womit auch die Herkunft der Grenze in der obigen Formel für Q für den Wechsel des Funktionsterms geklärt wäre. Mit Hilfe einer linearen Regression kann man die Approximation verbessern2, aber darauf kommt es gar nicht an, wie wir gleich sehen werden. Es sei noch einmal deutlich gesagt: Der Vorschlag von Herth/Arndts lautet, die Weyrauch-Näherung gerade außerhalb ihres Gültigkeitsbereichs zu verwenden und zwar dann, wenn \( ln \left( \frac{R}{{{A}_{RE}}} \right) \lt 1 \) ist.
Wie wirkt sich die Weyrauch-Näherung aus?
Die Approximation ist völlig unabhängig von der benutzen Reichweitenformel verwendbar und kann dann eingesetzt werden, wenn der Nenner \(ln\left( \frac{R}{{{A}_{RE}}} \right)\) lautet (und die oben angegebenen Grenzen eingehalten werden). Wie sich die Näherung auf den Verlauf des Graphen der Funktion Qs auswirkt, wenn man die Sichardtsche Reichweitenformel einsetzt, zeigen die nachstehenden Abbildungen.
Freie Oberfläche
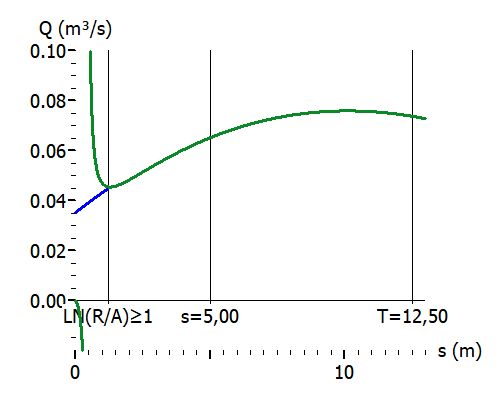
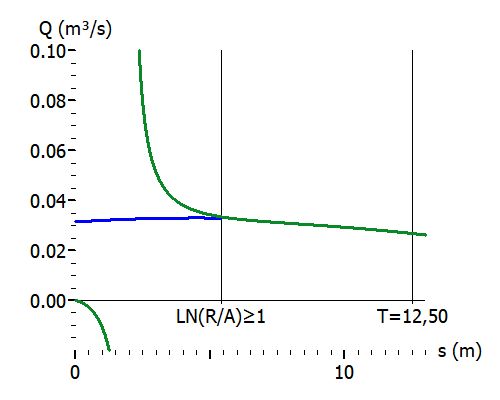
Gespannte Oberfläche
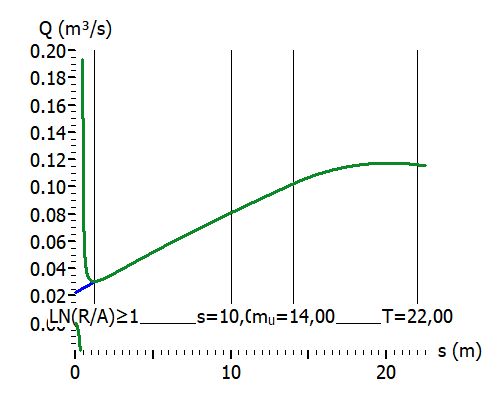
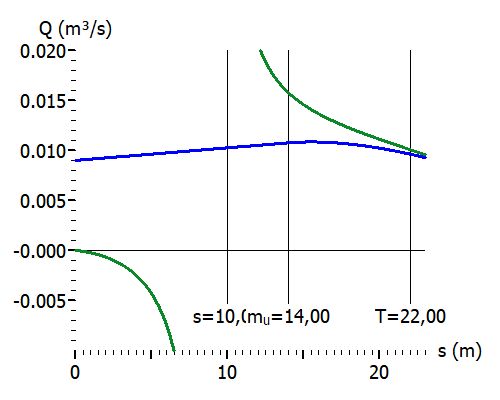
Grün: Q(s) mit Sichardt-Reichweite; Blau: Q(s) mit Weyrauch-Näherung.
frei typisch : s = 5 m, ARE = 30 m, k = 5E-4 m/s, H = T = 12,5 m, r = 0,3m.
frei ungültig: s = 10 m, ARE = 60 m, k = 1E-4 m/s, H = T = 12,5 m, r = 0,3m.
gespannt typisch : s = 5m, ARE = 30 m, k = 5E-4 m/s, H = T = 22 m, r = 0,3m.
gespannt ungültig: s = 10 m, ARE = 85 m, k = 1E-5 m/s, H = T = 22 m, r = 0,3m.
Hinweis: Die Graphen wurden mit GwR erzeugt und GwR benutzt hier die oben gezeigte
abschnittsweise definierte Funktion. Der Verlauf nach Weyrauch wird also nur für \(ln\left( \frac{R}{{{A}_{RE}}} \right) \lt 1\)
dargestellt.
Details zum Graphen der Weyrauch-Funktion
Mit Weyrauch-Funktion ist der Teil der abschnittsweise definierten Funktion s → Q(s) gemeint, der für \( ln\left( \frac{R}{{{A}_{RE}}} \right) < 1 \) gilt. Ich setze im Folgenden die Sichardtsche Reichweitenformel voraus; wenn man die nach Kussakin verwendet, ändert sich im Wesentlichen nichts.
Freie Oberfläche
Der Graph der Weyrauch-Funktion ist eine nach unten geöffnete Parabel; ihr Scheitelpunkt liegt bei \({{s}_{\max }}=H-\frac{4\cdot {{A}_{RE}}}{{{c}_{R}}\cdot \sqrt{k}}\), wobei mit cR der Faktor in der
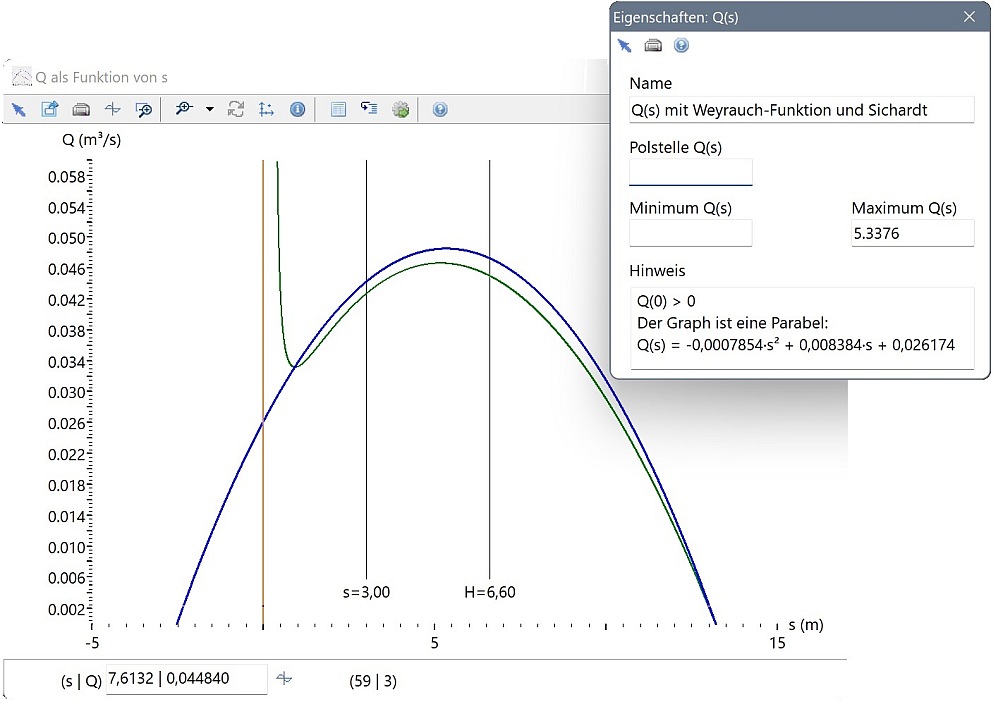
Gespannte Oberfläche
Der Graph der Weyrauch-Funktion ist eine Gerade mit positiver Steigung; auch hier ist Q(0) > 0.
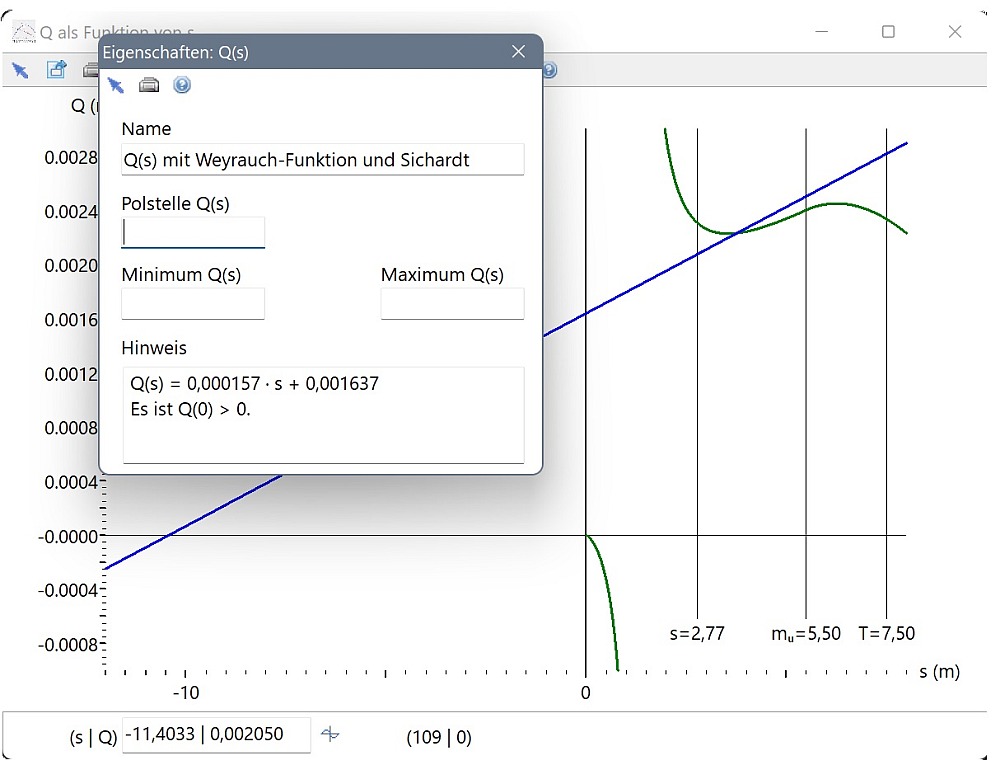
Ein Vorteil der Weyrauch-Approximation
Es ist nur ein Vorteil erkennbar: Die Polstelle wird beseitigt, Q(s) wird nicht mehr negativ.
... und viele Nachteile
Diesem Fortschritt stehen erhebliche Schwächen gegenüber.- Man erhält mit der Weyrauch-Formel (mit Sichardt-Reichweite) für s = 0 einen nicht verschwindenden Wasserandrang, denn es ist: \({{Q}_{s}}(0)=\frac{ 4 \cdot \pi \cdot {{A}_{RE}}\cdot H\cdot \sqrt{k}}{{c}_{R}} > 0\). Für Beispiel 1a (Herth/Arndts) ergibt das immerhin 126,45 m³/h.
-
An der Übergangsstelle der abschnittsweisen definierten Funktion tritt eine Unstetigkeit auf, denn für
\(ln\left( \frac{R}{{{A}_{RE}}} \right) = 1\Leftrightarrow s=\frac{e\cdot {{A}_{RE}}}{3000\cdot \sqrt{k}}\)
ist Q(s) nach Weyrauch berechnet um den Faktor \(\frac{2}{e}+0,25\approx 0,986\)
kleiner als der nach Dupuit-Thiem berechnete Wert für den Wasserandrang. Man könnte diese Unstetigkeit durch eine
genauere Approximation verringern, aber nicht beseitigen.
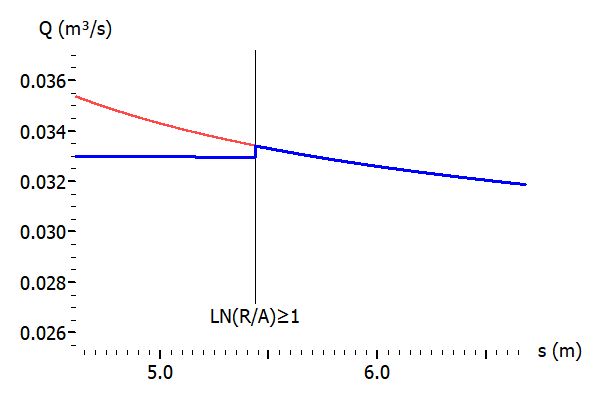
- Die Approximation ist nicht ganz so genau, wie die erste Grafik vielleicht vermuten lässt:
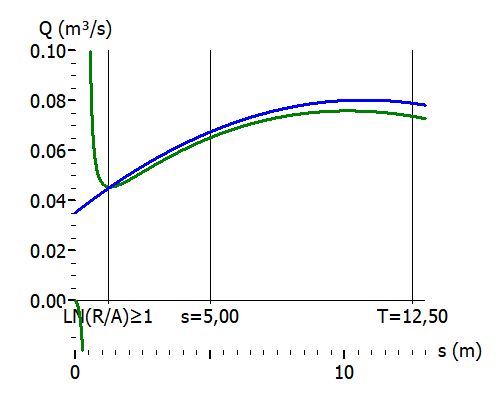 Grün: Q(s) mit Sichardt-Reichweite; Blau: Q(s) mit Weyrauch-Näherung, die hier durchgängig verwendet wird. Es findet also kein Wechsel des Funktionsterms bei \(ln\left( \frac{R}{{{A}_{RE}}} \right) \ge 1\) statt.Mit den Daten aus dem ersten Beispiel ergibt sich bei s = 5 m immerhin ein Unterschied bei Q von etwa 8,3 m³/h.
Grün: Q(s) mit Sichardt-Reichweite; Blau: Q(s) mit Weyrauch-Näherung, die hier durchgängig verwendet wird. Es findet also kein Wechsel des Funktionsterms bei \(ln\left( \frac{R}{{{A}_{RE}}} \right) \ge 1\) statt.Mit den Daten aus dem ersten Beispiel ergibt sich bei s = 5 m immerhin ein Unterschied bei Q von etwa 8,3 m³/h. - Oben hieß es: Bei bestimmten Bedingungen kann es vorkommen, dass "die Zuströmung Q mit kleiner werdenden Absenkungen
größer wird." Und die Weyrauch-Approximation wurde als Lösung für diese Anomalie angeboten. Aber auch sie versagt "bei
bestimmten Bedingungen", wie das folgende reale Beispiel aus dem Raum Gronau zeigt.
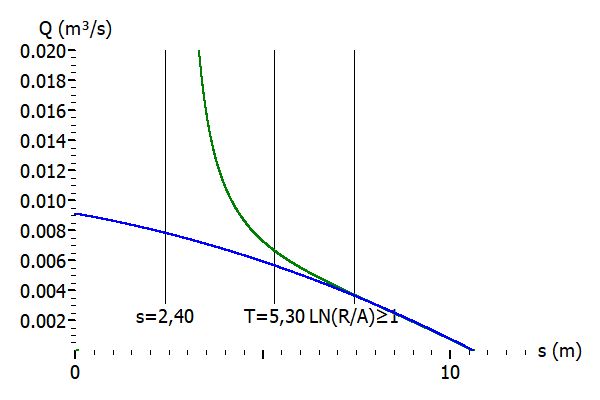 Daten: freie Oberfläche, k = 5E-5 m/s, s = 2,40 m, H = T = 5,3 m, r = 0,2 m. Vom Auftraggeber war eine vergleichende Berechnung bei kleiner werdender Absenktiefe verlangt.
Daten: freie Oberfläche, k = 5E-5 m/s, s = 2,40 m, H = T = 5,3 m, r = 0,2 m. Vom Auftraggeber war eine vergleichende Berechnung bei kleiner werdender Absenktiefe verlangt. - Die Berechnung von Q nach Weyrauch ist ein (versteckter) Zu- bzw. Abschlag zu Q und wie jeder andere Zu- oder Abschlag
stört er das Gefüge der Gleichungen, mit denen eine Grundwasserabsenkung berechnet wird. Er macht sich dadurch bemerkbar, dass
entweder die Absenkung in der Entfernung R nicht 0 ist oder die Absenkung in der Entfernung ARE nicht gleich s.
Welcher der beiden Fehler auftritt, hängt von der bei der Integration der Differentialgleichung nach Dupuit-Thiem
verwendeten Randbedingung ab. Das Folgende Beispiel zeigt den Unterschied.
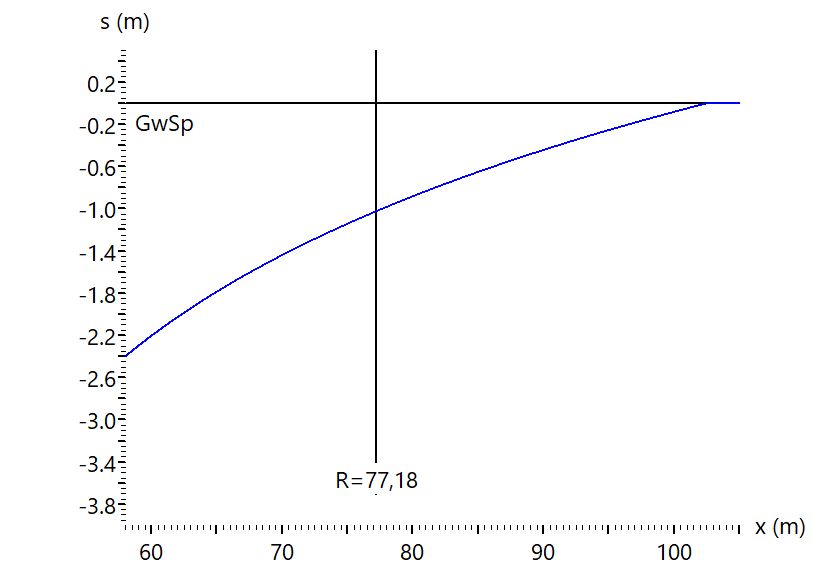
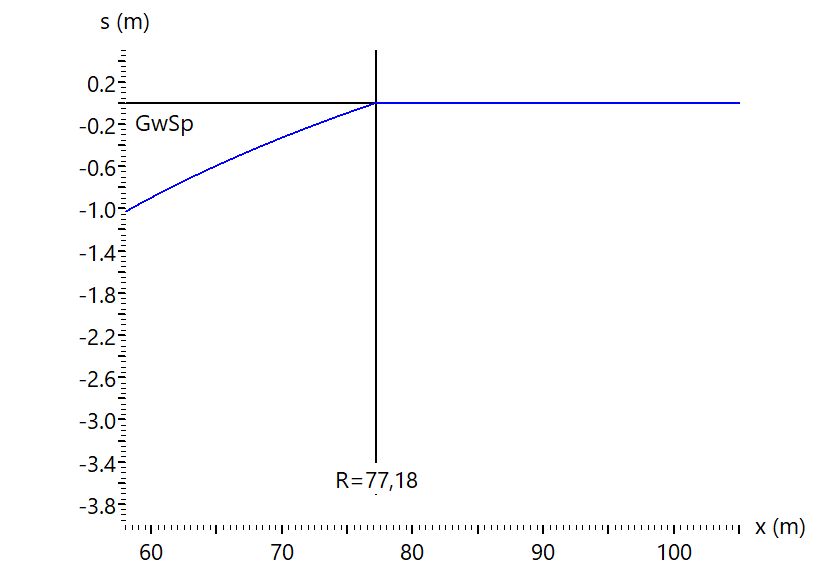
Ernüchterndes Fazit
Die Approximation ist einigermaßen genau in einem Bereich, in dem es heute keinen Vorteil bringt, sie zu benutzen3. Wird sie über ihren Gültigkeitsbereich hinaus fortgesetzt und insbesondere für Werte s mit \(ln\left( \frac{R}{{{A}_{RE}}} \right) \lt 1\) eingesetzt, so wird zwar die Polstelle von Qs beseitigt, aber die Anomalien bleiben bestehen. Mit der Weyrauch-Approximation kann allenfalls eine obere Grenze für den Wasserandrang bei flachen Absenkungen ermittelt werden. Kurz gesagt: Die in Herth/Arndts dargestellte Lösung für das Problem der Berechnung flacher Absenkungen ist so nicht haltbar und die sogenannte Weyrauch-Formel sollte zu ihrer Berechnung nicht angewandt werden - jedenfalls nicht ohne eine Analyse der Situation mit GwR.
Trotz dieser offenkundigen Schwächen wird die Approximation auch in Handbüchern benutzt. Stelzig4 behandelt eine Grundwasserabsenkung, bei der \(ln\left( \frac{R}{{{A}_{RE}}} \right) \approx 0,73\) ist und verwendet ohne weiteren Kommentar die Berechnung nach Weyrauch. Wegen der verbreiteten Verwendung in der Praxis ist die Weyrauch-Näherung auch in unserer Software verfügbar - kann aber abgeschaltet werden.
Weyrauch+Weber - ein Teil der Probleme ist gelöst!
Von Weber stammt der Vorschlag, die Reichweite unter Berücksichtigung des Ersatzradius wie folgt zu berechnen: $$R_{Weber} = {\sqrt{R^2 + A^2_{RE}}}$$ (Herth/Arndts (100), S. 97).
Für flache Absenkungen geht die Weber-Reichweite nicht gegen 0, wie die Sichardt-Reichweite, sondern gegen ARE. Kombiniert man die Weyrauch-Näherung mit der Reichweiten-Formel von Weber, dann erhält man einen Verlauf des Graphen der Funktion s → Q(s), der, wenigstens für flache Absenkungen, die Anforderungen (vgl. Anomalien) erfüllt. Ob die so ermittelten Wassermengen auch "richtig" sind ist eine andere Frage...
1. ∧ Persönliche Mitteilung von Dipl. Ing. Fritz Weyrauch.
2. ∧ Bei 20 Datenpunkten im Intervall [0, 0.4] erhält man y=2.0944x+0.2138 als optimale lineare Näherung.
3. ∧ Die Näherung war für Weyrauch nach eigenen Aussagen als Rechenvereinfachung gedacht - sie wurde schließlich in der Zeit der Rechenschieber entwickelt!
4. ∧ Stelzig, S., Wasserhaltung. In: Handbuch Geotechnik. Grundlagen – Anwendungen – Praxiserfahrungen; Hrsg. Conrad Boley, Springer Vieweg (eBook) 2019), 261-327.
