Nachweis einer Grundwasserabsenkung – noch ein Lehrbuchbeispiel

» Diesen Beitrag als PDF-Datei herunterladen.

Man erbringt den Nachweis dafür, dass eine Grundwasserabsenkung ausreichend dimensioniert ist, indem man die Wassermenge berechnet, die für das Erreichen des Absenkziels in "ungünstigen Punkten" benötigt wird und dann überprüft, ob das Leistungsvermögen der Brunnen dafür ausreicht.

In diesem Text möchte ich zeigen, dass diese gängige Praxis nicht immer erfolgreich ist. Es kann nämlich durchaus sein, dass das Absenkziel in allen ausgewählten Punkten erreicht wird und es trotzdem Bereiche am Grubenrand gibt, in denen es verfehlt wird.

Ich verwende ein in der Literatur dargestelltes Berechnungsbeispiel¹. Solche Beispiele sind für mich aus dem einfachen Grund wichtig, weil sich daran überprüfen lässt, inwieweit die Ergebnisse mit ProAqua übereinstimmen und wie sich eventuelle Abweichungen erklären lassen.

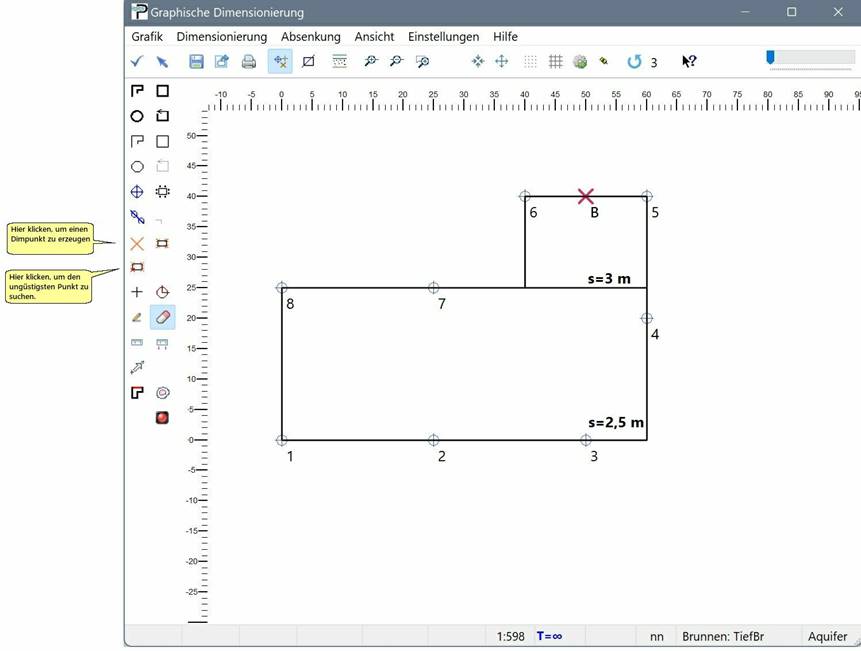
Es handelt sich um eine L-förmige Baugrube mit zwei verschiedenen Absenktiefen; die größere Grube hat die Maße 60 m × 25 m bei einer Absenktiefe von 2,5 m. Die kleinere, anliegende Grube, hat die Maße 20 m × 15 m; die Absenktiefe beträgt 3 m. Die Tiefe des Wasserstauers ist nicht bekannt, Tiefen sind auf den Ruhewasserspiegel bezogen. Es wird ein Zuschlag von 10 % für das Leerpumpen des Absenktrichters und pauschal von 25 % für unvollkommene Brunnen angesetzt.

Oberfläche		frei
Absenktiefe	s	2,5 m / 3 m
Baugrube (rechteckig)		60 m x 40 m
Abstand Brunnen-Grube		0 m
k-Wert	k	0,001 m/s
Eintauchtiefe der Brunnen	H	6,6 m
Brunnendurchmesser	d	0,60 m

Die Koordinaten der 8 Brunnen werden mitgeteilt, so dass ein exakter Nachvollzug der Berechnung mit ProAqua möglich ist.

Phase 1: Ermittlung des Wasserandrangs und der benötigten Brunnenleistung

 

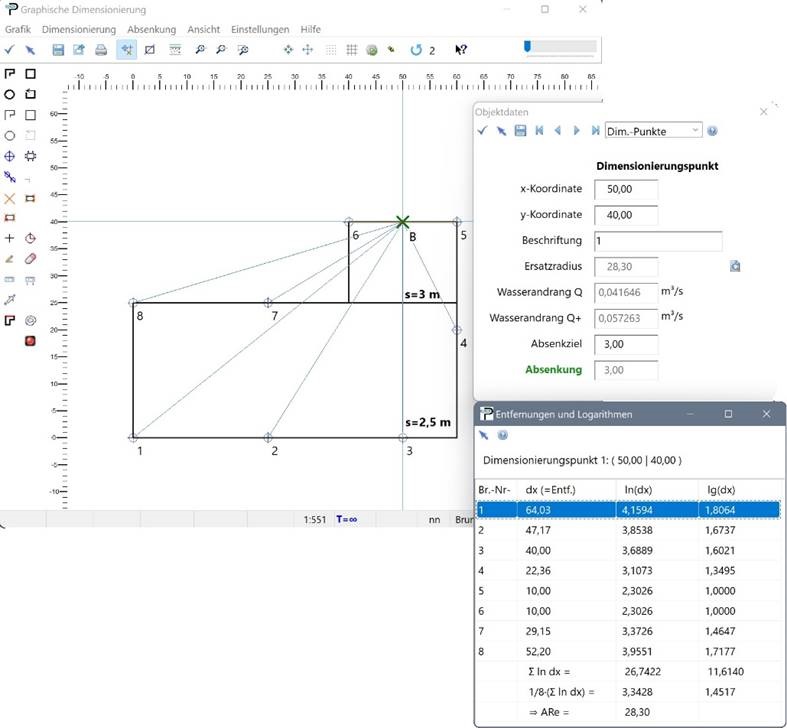
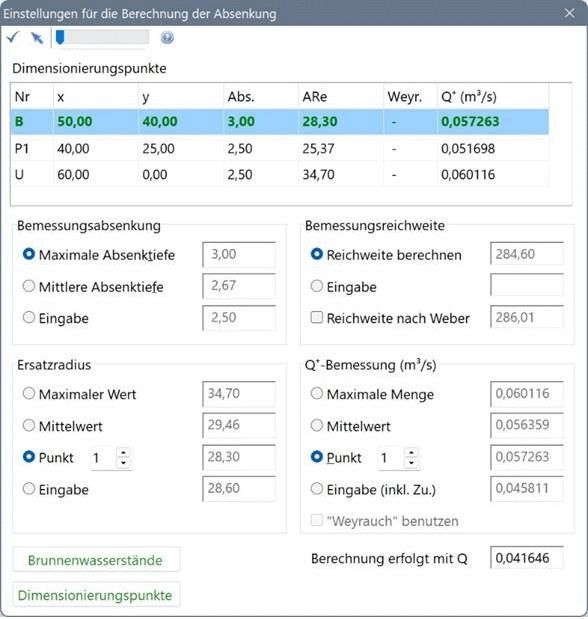
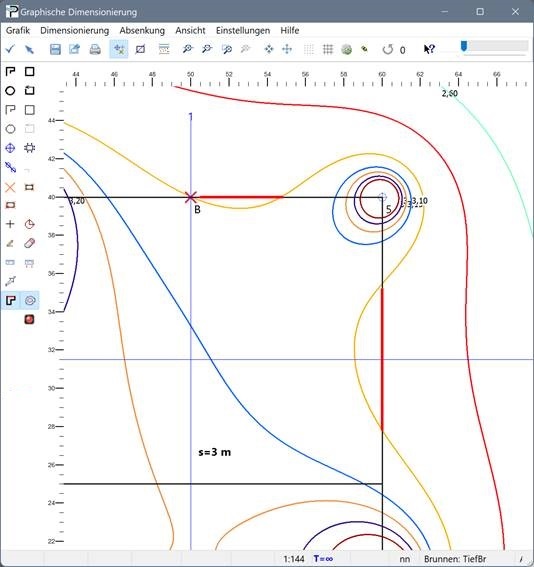
Als ungünstigster Punkt wird B(50 | 40 ) angenommen („dabei sollte der mittlere Abstand zu den Einzelbrunnen so groß wie möglich sein“, S. 287), dort wird ein Dimensionierungspunkt mit dem Absenkziel s = 3 m gesetzt. Daraus folgt, dass die Reichweite R = 284,60 m beträgt.

Jetzt ist der Ersatzradius A_Re im Punkt B zu berechnen; er ergibt sich aus den Entfernungen x_i von B zu den Brunnen nach der Formel:
$$A_{Re}=e^{\frac{1}{n} \cdot \sum \limits_{i=1}^{n} ln \left( x_i \right)}$$

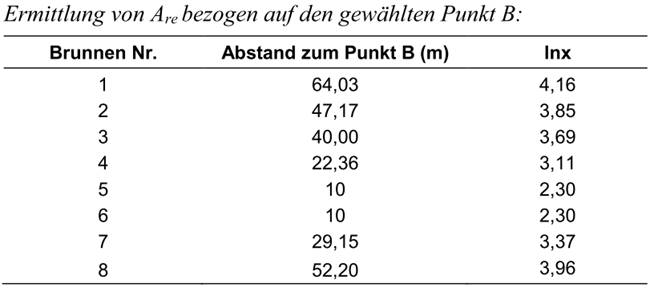
Der Mittelwert der Summe der Logarithmen beträgt 3,3425 ~ 3,343 und damit ist A_Re= 28,303... m. Bei der freien Oberfläche gilt:
$$Q=\frac{\pi \cdot k \cdot \left( H^2 - h^2 \right)}{ln\left( \frac{R}{r} \right) }$$ Für r wird A_Re eingesetzt:
$$Q=\frac{\pi \cdot k \cdot \left( H^2 - h^2 \right)}{ln\left( \frac{R}{A_{Re}} \right) }$$

h = H – s_max = 3,6 m und damit Q_B = 0,041647…m³/s.
Berücksichtigt man noch die Zuschläge, so gilt:
Q_maxB = Q_B·1,1 ·1,25 = 0,458127… m³/s ·1,25 = 0,057265… m³/s.²

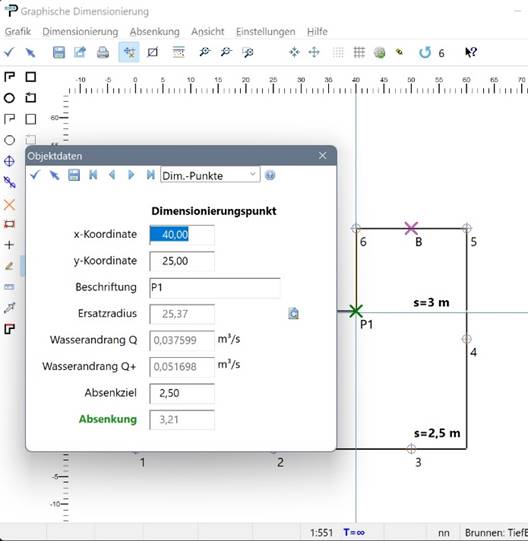
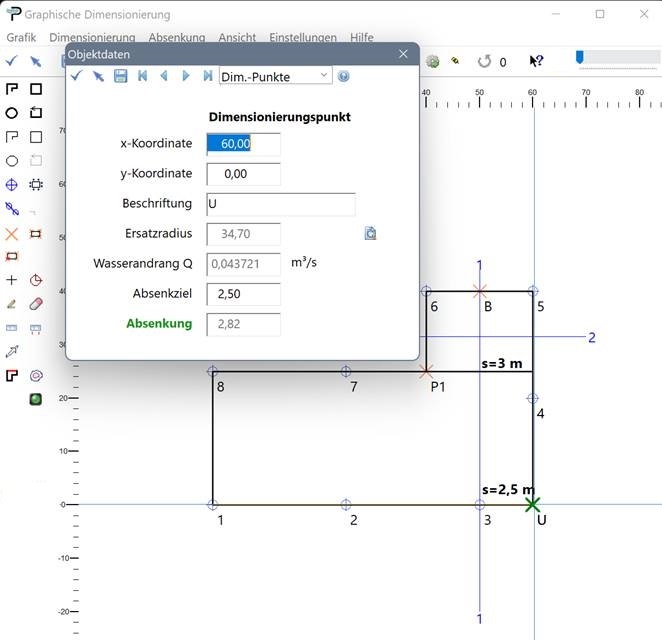
Soweit die Ergebnisse der Berechnungen im Handbuch. Was erhält man mit ProAqua? Durch einen Rechtsklick über B öffnet sich der in der folgenden Abbildung gezeigte Dialog mit allen relevanten Daten eines Objekts in einer ProAqua-Zeichnung. Klickt man auf das Symbol neben dem Feld mit dem Ersatzradius, so erscheint eine Tabelle der Entfernungen von B zu den Brunnen, mit der die Berechnung von A_Re nachvollzogen werden kann. Die betreffenden Strecken werden in der Grafik dargestellt.

Hier eine Zusammenstellung der Ergebnisse, die eine nahezu vollständige Übereinstimmung zeigt:

		Beispiel	ProAqua
Reichweite	R	284,60 m	284,60 m
Ersatzradius in B	ARe	28,30 m	28,30 m
Wasserandrang in B ohne Zuschläge	QB	0,0418 m³/s	0,041646 m³/s
Wasserandrang in B mit 10 % Zuschlag	Qz1	0,046 m³/s	0,045811 m³/s
Wasserandrang in B mit allen Zuschlägen	QmaxB	0,057 m³/s	0,057263 m³/s
Zahl der Brunnen	n	8	8
Erf. Brunnenleistung qBr = QmaxB/8	qBr	0,0071 m³/s	0,007158 m³/s

Phase 2: Reicht das Fassungsvermögen der Brunnen aus?

Die erste Phase der Dimensionierung ist mit der Bestimmung des Wasserandrangs in B und der erforderlichen Brunnenleistung abgeschlossen. Nun gilt es nachzuweisen, dass die Wassermenge auch gefördert werden kann; dazu wird die Brunnenergiebigkeit berechnet.

Es gilt: $$s_{EB} = h -\sqrt{h^2-\frac{1,5 \cdot q \cdot ln \left( \frac{b}{r} \right)}{\pi \cdot k}}$$

Bei B ist der Brunnenabstand gleich 20 m, für q wird Q_z1 eingesetzt; damit folgt für s_EB = 1,76 m. Die Höhe der benetzten Filterfläche h’ berechnet sich dann zu:

h‘ = H – s_max - s_EB = 6,60 m – 3 m – 1, 76 m = 1,84 m ⇒ q_mögl = 0,0073 m³/s

In ProAqua gibt es zwei Wege, um diese Rechnung nachzuvollziehen; ich werde beide zeigen.

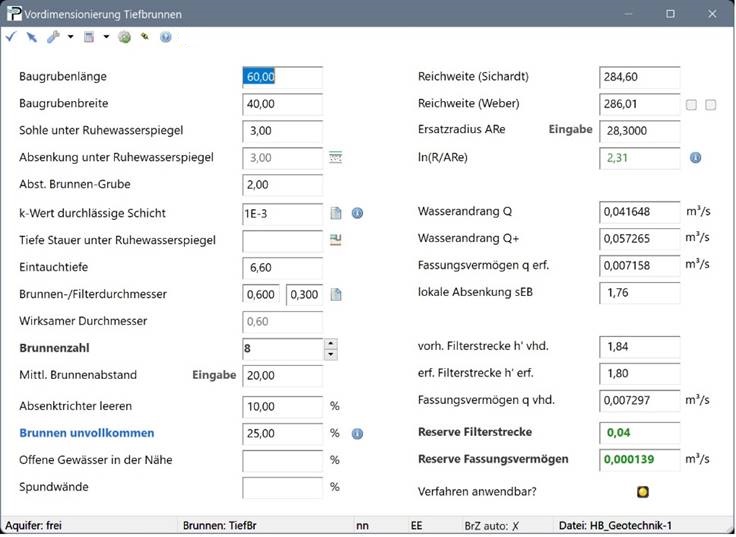
Weg 1: Nachweis in der Vordimensionierung

Wir öffnen die Vordimensionierung und überschreiben die berechneten Werte durch eine Eingabe. Ein Rechtsklick öffnet das Kontextmenü, in dem sich die Befehle zur Eingabe eigentlich berechneter Werte befinden. Wir ersetzen:

• den Wert für A_Re durch den für B gültigen Wert (A_Re = 28,30 m)
• den Wert für den mittleren Brunnenabstand durch den für die Umgebung von B angenommen Abstand (d = 20 m)
• den Wasserandrang Q durch den für B ermittelten Wert (Q = 0,057263 m³/s).

ProAqua markiert diese Ersetzungen durch das Label „Eingabe“ vor dem jeweiligen Eingabefeld. Durch die Auswahl von "Wasserandrang berechnen" (entsprechend für die anderen Größen) ist eine Rückkehr zu den berechneten Werten möglich.

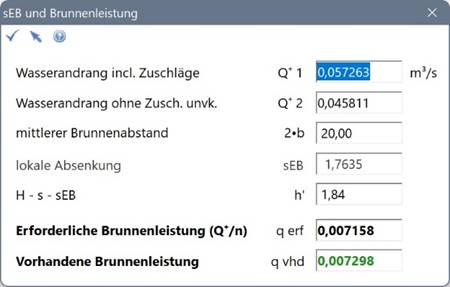
Als Ergebnis liest man ab:

		Beispiel	ProAqua
Lokale Absenkung	sEB	1,76 m	1,76 m
Benetzte Filterfläche	h'	1,84 m	1,84 m
Leistungsvermögen der Brunnen	qmögl	0,0073 m³/s	0,007297 m³/s

Da q_mögl > q_Br, wenn der Unterschied auch minimal ist, gilt der Nachweis erbracht, dass die Absenkung mit 8 Brunnen erfolgreich durchgeführt werden kann.

Weg 2: Nachweis in der Grafik

Der gleiche Nachweis kann auch direkt in der Grafik geführt werden. Im Menü Dimensionierung gibt es seit ProAqua 4.0 (15.09.22) den Menüpunkt "sEB und Brunnenleistung". Es öffnet sich ein Dialog, in dem die in der Grafik mit der Mehrbrunnenformel ermittelten Werte schon eingetragen sind – abhängig von der Wahl, die in der Dimensionierung getroffen wurde.

Fazit

Die Übereinstimmung der Berechnungen ist sehr gut. Systematische Abweichungen ergeben sich z. B. dadurch, dass in vielen in der Literatur zu findenden Beispielen Werte auf zwei Stellen gerundet werden und mit diesen gerundeten Werten weiter gerechnet wird, während ein Computerprogramm in der Regel nur für die Anzeige rundet, aber intern mit allen verfügbaren Stellen rechnet.

Phase 3: Nachweis in weiteren Punkten

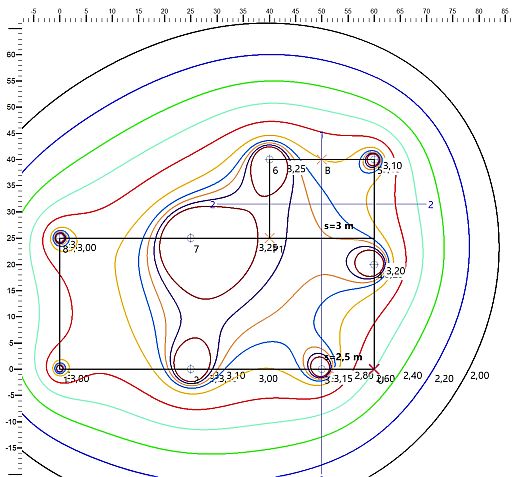
Damit ist die zweite Phase der Dimensionierung abgeschlossen. Üblicherweise schließt sich in einer dritten Phase die Überprüfung in weiteren Punkten an. Im Beispiel wird die Absenkung im Punkt P1(40 | 25) nachgerechnet.

Als lokaler Ersatzradius wird A_Re = 25,28 m mitgeteilt, ProAqua berechnet A_Re = 25,37 m. Damit lässt sich die Absenkung in P1 berechnen, der Autor gibt an: s_P = 3,21 m. Trotz der kleinen Abweichung bei A_Re, auch hier stimmt die berechnete Absenkung genau überein.

Die Karte der Isolinien der Wasserstände kann durch einen Klick auf das Symbol angezeigt werden – konfiguriert wird die Karte im Dialog "Dimensionierung".

Dieser Dialog ist vor allem wichtig, wenn es verschiedene Absenktiefen gibt. In der Regel wird man mehrere Dimensionierungspunkte setzen und die Maximalwerte wählen. Um das Beispiel nachzuvollziehen, müssen jedoch der Wasserandrang in B und der Ersatzradius in B für die Berechnung zugrunde gelegt werden.

Probleme? Probleme!

Die Absenkung wurde in P1 überprüft, das Absenkziel wird erreicht, also ist alles gut?

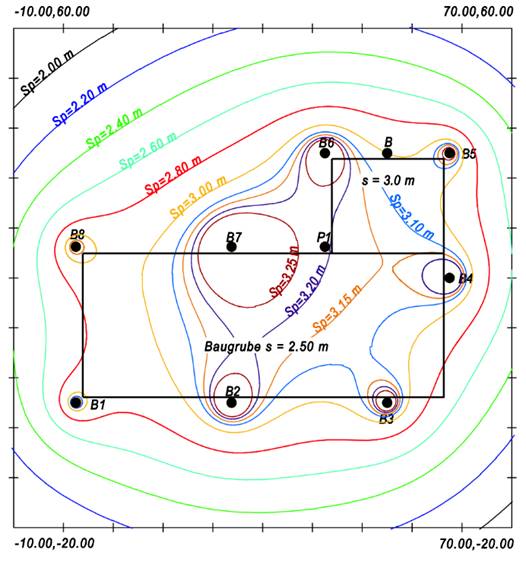
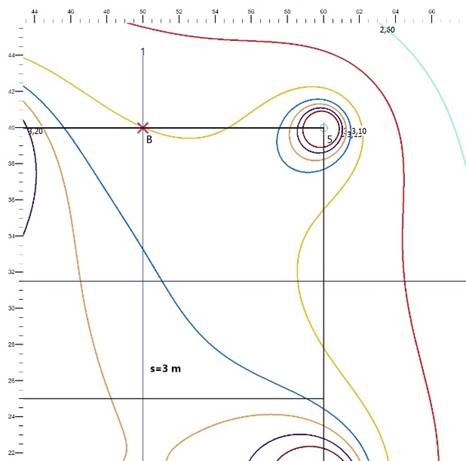
Schaut man sich die Wasserkarte etwas genauer an, so fällt auf, dass die 3 m-Linie (das ist die Linie, die durch B verläuft) die Baugrube schneidet. Eine Ausschnittsvergrößerung zeigt das deutlicher:

Eine Schnittlinie durch B zeigt, dass der Wasserstand geringfügig über der Baugrubensohle liegt. Seit ProAqua 4.0 kann man die Absenkung auf dem Grubenrand untersuchen. Dazu klickt man auf das Symbol, das einen Grubenumriss mit einer roten Linie zeigt (es befindet sich in der linken Spalte der Werkzeugpalette und ist in der folgenden Abbildung blau hinterlegt).

In den hier rot markierten Bereichen wird das Absenkziel auf dem Grubenrand nicht erreicht. Beachten Sie die rote Ampel in der Grafik (sie ist auch schon in Abbildung 1 zu sehen); sie weist auf Probleme bei der Berechnung der Absenkung hin. Klickt man darauf, so erscheint ein Dialog, der die Ergebnisse zusammenfasst.

Wie kommt es zur Unterdimensionierung?

Zur Unterdimensionierung kann es kommen, wenn der Wasserandrang zu klein ist – weil B nicht der wirklich ungünstigste Punkt ist – oder weil die die Brunnen das erforderliche Wasser nicht fassen können.

ProAqua kann den ungünstigsten Punkt auf dem Grubenrand (auch von inneren Gruben) suchen. Dazu ist auf das Symbol unter dem für einen Dimensionierungspunkt (vgl. Abbildung 1) zu klicken. Bei der Suche wird die Tiefe der jeweiligen Linie beachtet.

Es zeigt sich: Der ungünstigste Punkt ist nicht B wie angenommen, sondern U(60 | 40) auf der Ecke unten rechts; sein Ersatzradius A_Re ist mit 34,7 m deutlich größer als der im Punkt B. Wählt man seinen Wasserandrang Q_U als Bemessungswassermenge, dann gelingt die Absenkung doch noch – und die Ampel ist jetzt grün.

Fazit

Es reicht nicht aus, einen "ungünstigen Punkt" nach Augenmaß festzulegen und damit eine Grundwasserabsenkung zu dimensionieren. Auch wenn man auf jeden Eckpunkt der Baugrube einen Dimensionierungspunkt setzt, kann es sein, dass der wirklich ungünstigste Punkt nicht erfasst wird³. In jedem Fall sollte dieser Punkt mit der entsprechenden Funktion in ProAqua gesucht werden. In unserem Beispiel wird das Absenkziel nur um Zentimeter verfehlt. In anderen Fällen können die Abweichungen so groß sein, dass man sie nicht tolerieren wird.

Ein Nachtrag

Nach Herth/Arndts darf bei der Berechnung der Isolinien und bei der Berechnung von s_EB ein Zuschlag für unvollkommene Brunnen nicht angesetzt werden, "da die Zuströmung von unten keinen Einfluß auf die Krümmumg der Absenkkurve hat" (S. 83; vgl. S. 217). Stelzig beachtet dies (vgl. S. 289) und setzt bei der Berechnung von s_EB und der Absenkung in P1 den Zuschlag von 25 % für unvollkommene Brunnen nicht an.

In den Versionen bis einschließlich 4.3 von ProAqua wurden die Isolinien grundsätzlich ohne Zu- oder Abschläge berechnet; auch ein Zuschlag von 10 % für das Leerpumpen des Absenktrichters wurde nicht angesetzt. Wie die sehr gute Übereinstimmung der "Wasserkarten" zeigt, wurde auch die im Handbuch abgedruckte Version ohne Einbeziehung der Zuschläge berechnet. Ein Verdacht stellt sich ein: Könnte es sein, dass ProAqua hier mit sich selbst verglichen wurde?

---