Nachweis einer Grundwasserabsenkung – gespannte Oberfläche
» Diesen Beitrag als PDF-Datei herunterladen.
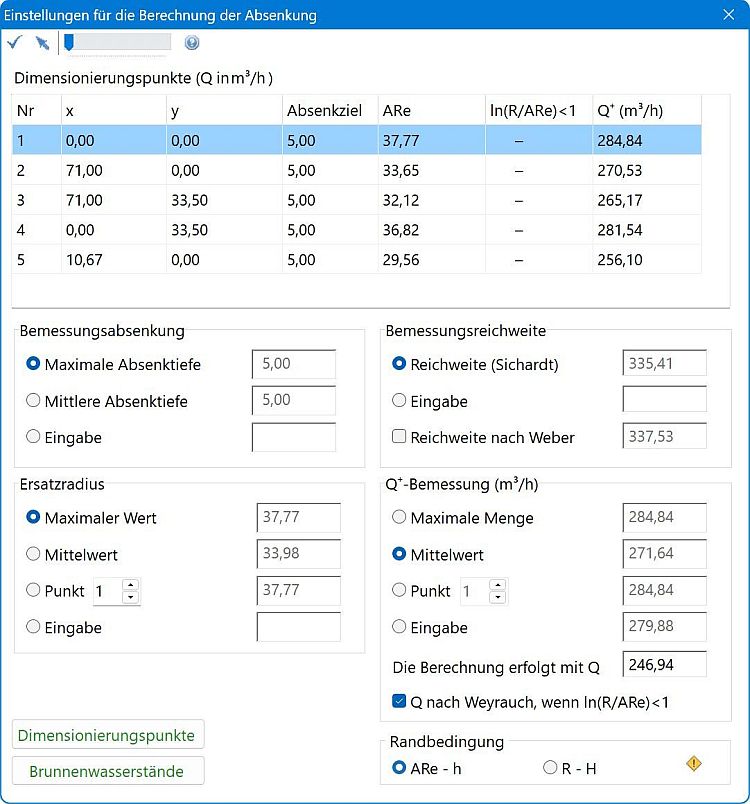
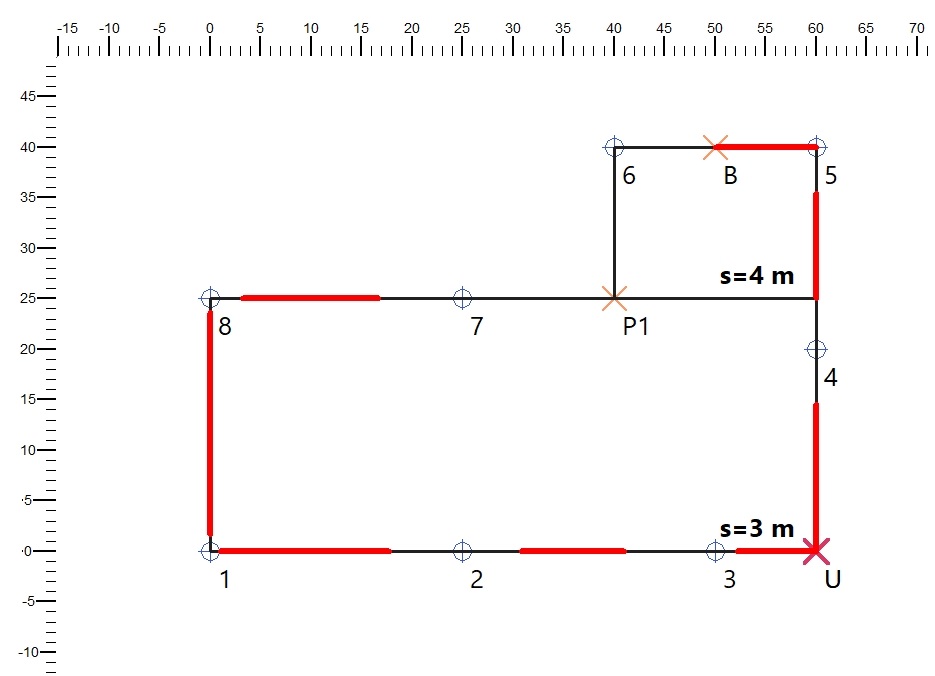
Das im Anschluss an das im Text "Nachweis einer Grundwasserabsenkung" behandelte Beispiel einer Absenkung bei gespannter Oberfläche ist wesentlich knapper dargestellt1. Baugrube und Brunnenanordnung bleiben gleich, die Absenktiefen werden vergrößert. Auch die Lage der Nachweispunkte B und P1 bleibt gleich.
Solche Beispiele sind für mich aus dem einfachen Grund wichtig, weil sich daran überprüfen lässt, inwieweit die Ergebnisse mit ProAqua übereinstimmen und wie sich eventuelle Abweichungen erklären lassen.
| Oberfläche | gespannt | |
| Tiefe Stauer | T | 7,50 m |
| k-Wert | k | 0,00005 m/s |
| Mächtigkeit der wasserführenden Schicht | m | 2,0 m/s |
| Absenktiefe | s | 3 m / 4 m |
| Baugrube (rechteckig) | 60 m x 40 m | |
| Abstand Brunnen-Grube | 0 m | |
| Eintauchtiefe der Brunnen | H | 7,5 m |
| Brunnendurchmesser | d | 0,60 m |
In einer Vorüberlegung (die mit ProAqua nicht nachvollzogen werden kann) wird die erforderliche Entspannung mit se max = 2,77 m ermittelt. Mit diesem Wert wird die Anlage dimensioniert. Die Ergebnisse werden (zusammen mit den benutzten Formeln) mittgeteilt:
| Beispiel | ProAqua | ||
| Reichweite | R | 58,76 m | 58,76 m |
| Ersatzradius für B | ARe | 28,30 m | 28,30 m |
| h = H - se max | m | 4,73 m | 4,73 m |
| Wasserandrang | Qmax B | 0,0021 m³/s | 0,002112 m³/s |
| Erforderliche Brunnenleistung | qBr | 0,00026 m³/s | 0,000264 m³/s |
| Lokale Absenkung (mit b = 10 m berechnet) | sEB | 2,21 m | 2,2094 m |
| Benetzte Filterfläche | h' = h - sEB | 2,52 m > 2 m | 2,5206 m |
| Leistungsvermögen der Brunnen (h' = 2 m) | qmögl | 0,0018 m³/s | 0,001777 m³/s |
Hinweis: Da ln(R/ARe) ≈ 0,73 < 1 ist, wird die sogenannte Weyrauch-Näherung zur Berechnung von Q benutzt – so empfehlen es Herth/Arndts und so verfährt auch ProAqua. Näheres zu diesem Thema finden Sie in dem Text "Die Weyrauch-Näherung". Wie man sieht, stimmen die Ergebnisse überein.
Zu Unterschieden kommt es dann beim „Nachweis der Entspannung zu einem beliebigen Punkt“ (S. 295). Wie im Beispiel für den freien Spiegel wird der Punkt P1(40 | 25) gewählt; mitgeteilt wird; yP = 4,36 m ⇒ sP = H – yP = 3,14 m.
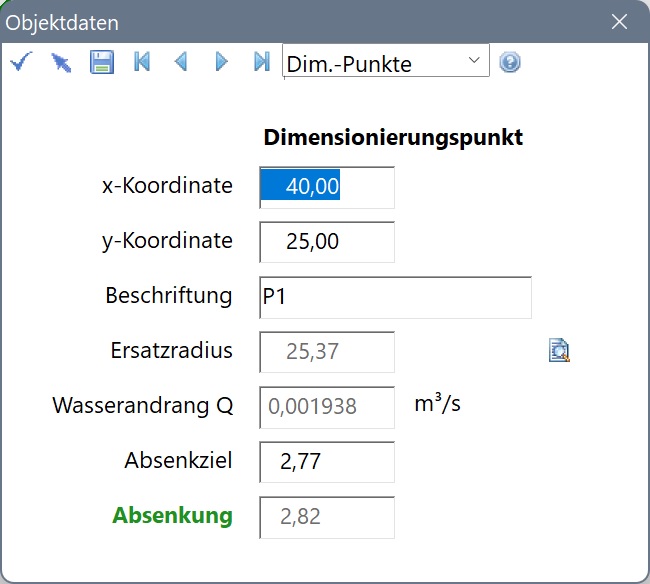
ProAqua ermittelt sP = 2,82 m – ein gravierender Unterschied! Ein Fehler? Eine genauere Analyse ergab (lesen Sie bitte noch einmal den zweiten Absatz oben) Folgendes.
Analyse der Unterschiede
Für die Berechnung der Absenkung mit der Mehrbrunnenformel kann man zwei verschiedene Randbedingungen benutzen:
1. x1 = xP, y1 ist gesucht, x2 = ARe, y2 = H – s = h
2. x1 = xP, y1 ist gesucht, x2 = R, y2 = H
Für die Absenkung sP ergibt sich damit jeweils:
$$ \begin{align} s_{P,1} &= s- \frac{Q}{2 \cdot \pi \cdot k \cdot m} \cdot ln\left( \frac{x_P}{A_{Re}} \right) \\ s_{P,2} &= \frac{Q}{2 \cdot \pi \cdot k \cdot m} \cdot ln\left( \frac{R}{x_P} \right) \end{align} $$ProAqua benutzt seit längerem für den gespannten Leiter die Randbedingungen nach 2. weil dann eine Rechenoperation weniger ausgeführt werden muss; Stelzig benutzt (wie auch Herth/Arndts) die Randbedingungen nach 1.
Wie man leicht nachrechnet gilt sP,1 = sP,2 – wenn man für Q die Formel nach Dupuit/Thiem einsetzt.
Wird Q allerdings nach Weyrauch berechnet, so ergibt sich die Differenz zu:
$$s_{P,1}-s_{P, 2} = s \cdot \left( 1- \left( 2 \cdot \frac{A_{Re}}{R} +\frac{1}{4} \right) \cdot ln \left( \frac{R}{A_{Re}} \right) \right)$$
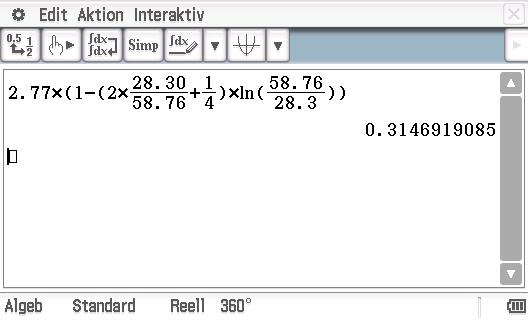
denn ln(R/ARe) kann nicht mehr gekürzt werden. Setzt man die Werte entsprechend ein, so erhält für die Differenz
sP,1 - sP,2 = 3,14 m - 2,82 m = 0,32 m. Damit ist die Ursache für den Unterschied und seine Größe gefunden.
Auch eine Mittelwertbildung verursacht das gleiche Problem
Dieses Problem tritt bei jeder von Duit/Thiem abweichenden Festlegung der Wassermenge auf. Wenn man also in ProAqua im Dimensionierungsdialog des Grafikmoduls die Bemessungswassermenge als Mittelwert der Wassermengen der Dimensionierungspunkte wählt oder die Bemessungswassermenge frei eingibt, dann werden sich die berechneten Absenkungen abhängig von der gewählten Randbedingung ändern.
Und welcher Wert ist jetzt richtig?
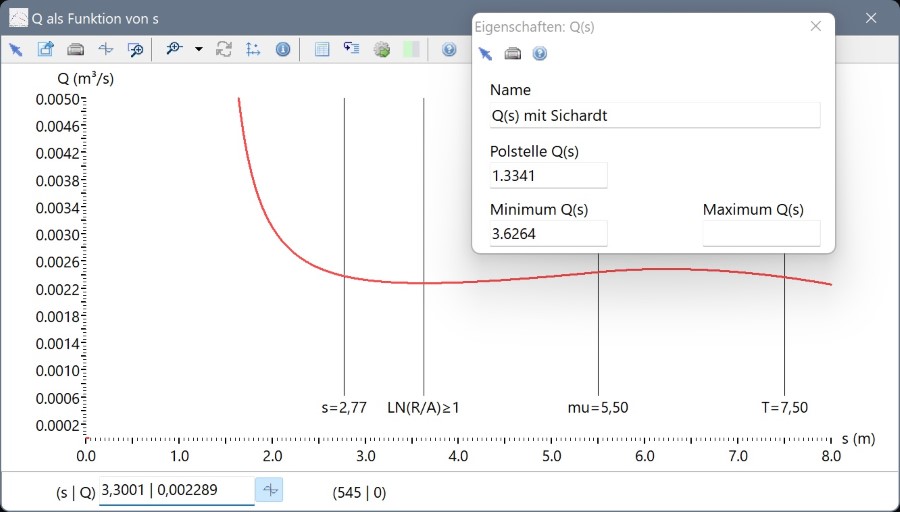
Mit GwR kann man den Graphen der Funktion s → Q(s) darstellen (erstes Bild in der folgenden "Lightbox"). Es gibt ein Minimum, das sich, wie man zeigen kann, an der Stelle mit ln(R/ARe) = 1 befindet: links davon steigt der Graph gegen unendlich, für s < 1,33 m werden die Werte negativ. Näheres zu diesem Verlauf finden Sie im Text "Anomalien von Q in Abhängigkeit von s". Was bewirkt die "Weyrauch-Näherung" (zweites Bild in der "Lightbox")?
Die Weyrauch-Näherung wird nur für ln(R/ARe) < 1 benutzt; der Weyrauch-Graph verläuft zwar linear fallend, ergibt aber für s = 0 einen positiven Wasserandrang – was natürlich eklatant falsch ist.
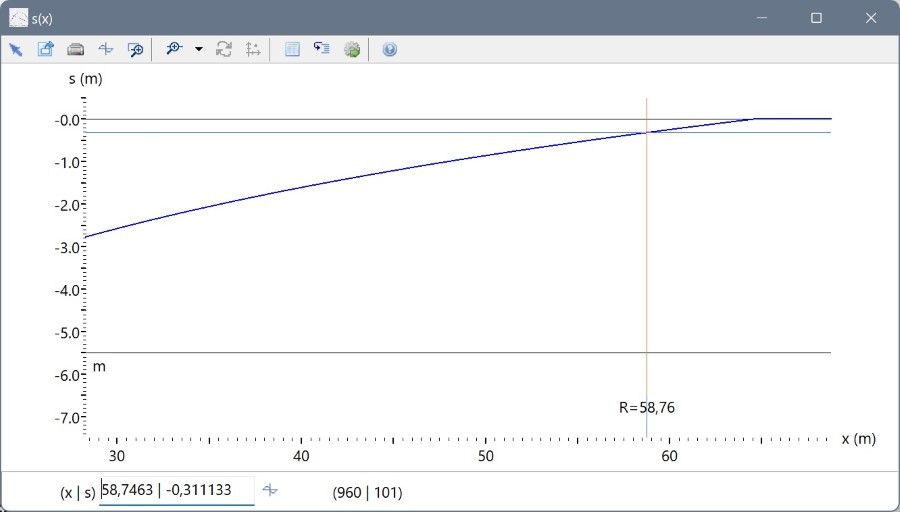
Stellt man den Verlauf von x → s(x) mit Q nach Weyrauch graphisch dar, so sieht man, dass bei Benutzen der 1. Randbedingung in R die Absenkung noch nicht 0 ist.
Geht man zur 2. Randbedingung über (2. Bild), ist zwar s(R) = 0, aber dafür ist s(ARe) ≠ s.
Und was ist nun richtig? Keiner der beiden Werte ist "richtig". Wenn Q nach der Weyrauch-Formel bestimmt wird, können Sie zwischen einem der beiden Fehler wählen: Entweder ist s(R) falsch oder s(ARe) ist falsch und infolge dessen sind auch alle Werte sP verschieden. Durch die Berechnung des Wasserandrangs nach Weyrauch wird das Gefüge der Gleichungen gestört und man erhält bestenfalls näherungsweise richtige Ergebnisse.
In einer früheren Fassung hieß es: “Letztlich ist die von s abhängige Reichweitenformel nach Sichardt die Ursache der Fehler. …“ Aber das ist falsch; der Fehler ist von der Reichweitenformel unabhängig und allein der Abweichung von der Wassermenge nach Dupuit/Thiem geschuldet.
Weitere Probleme
Wie im Beispiel zum freien Leiter gezeigt, ist B nicht der ungünstigste Punkt und deshalb wird das Absenkziel zumTeil deutlich (im ungünstigsten Punkt U um etwa 1 m) verfehlt. Weil dieser Nachweis völlig analog verläuft, wird das nicht weiter ausgeführt.
